Las Ecuaciones Diferenciales Reducibles a Homogéneas surgieron como una extensión natural del estudio de las Ecuaciones Diferenciales Homogéneas de primer orden, cuyo desarrollo se remonta a los siglos XVII y XVIII, en el contexto de la fundación del cálculo diferencial e integral por parte de Isaac Newton y Gottfried Wilhelm Leibniz.
Siglo XVII–XVIII: Con el surgimiento del cálculo, los matemáticos comenzaron a estudiar ecuaciones que relacionaban una función con su derivada. Entre ellas, las Ecuaciones Homogéneas (en el contexto de funciones racionales Homogéneas de igual grado) fueron de las primeras en analizarse debido a su estructura algebraica particular que permite su resolución mediante el cambio de variable.
Método de reducción a Homogéneas: Este método surgió como una técnica de transformación útil cuando una Ecuación Diferencial no es Homogénea en su forma original, pero puede ser convertida en una Homogénea mediante un cambio de variables adecuado.
Este enfoque fue sistematizado en el siglo XVIII y XIX por matemáticos como Leonard Euler, Joseph-Louis Lagrange y otros desarrolladores del cálculo diferencial.
Hoy en día, el método de reducción a Homogéneas es una técnica estándar que se enseña en cursos de Ecuaciones Diferenciales Ordinarias en el nivel universitario.
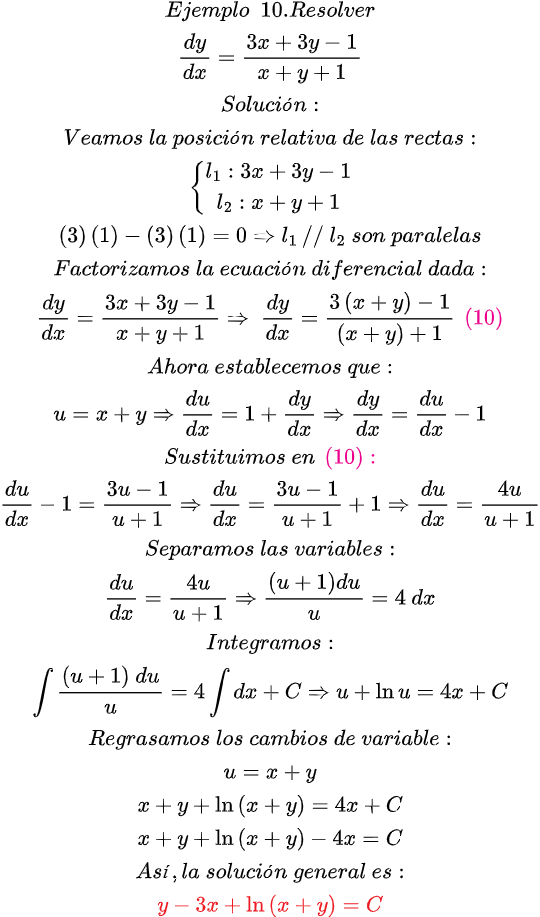
En esta publicación exploraremos paso a paso la solución de 10 ejercicios cuidadosamente seleccionados de Ecuaciones Diferenciales Reducibles a Homogéneas.















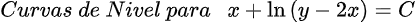

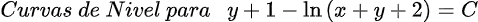



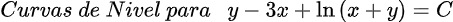

Me siento afortunado de contar con una comunidad tan entusiasta, generosa y comprometida. Sus comentarios, sugerencias y muestras de cariño han sido una fuente inagotable de motivación e inspiración para seguir creando y creciendo juntos.
Gracias por ser parte de este viaje, por su confianza y por ayudarme a mejorar cada día. Sin ustedes, nada de esto sería posible. ¡Sigamos compartiendo ideas, aprendizajes y buenos momentos en Hive Blog!.
Un fuerte abrazo,
Gary Nuñez .
DIOS LOS BENDIGA

1.- A. Kiseliov, M. Krasnov y G. Makarenko. Problemas de Ecuaciones Diferenciales Ordinarias. Editorial MIR, 1984.
2.- Acero, Ignacio. Ecuaciones Diferenciales Teoría y Problemas. Editorial Tébar, 2007.
3.- Boyce, William E., DiPrima, Richard C., Meade, Douglas B. Ecuaciones Diferenciales Elementales y Problemas de Valores en la Frontera. Editorial Wiley, 2012.
4.- C. Henry Edwards, David E. Penny. Ecuaciones Diferenciales. Editorial Pearson Educación de México, 2001.
5.- Earl D. Rainville, Phillip E. Bedient, Richard E. Bedient. Ecuaciones Diferenciales. Editorial Pearson Educación, 1997.
6.- G. Baranenkov, B. Demidovich, V. Efimenko, S. Kogany, G. Lunts, E. Porshneva, E. Sichova, S. Frolov, R. Shostak y A. Yanpolskí. Problemas y Ejercicios de Análisis Matemático. Editorial MIR, 1967.
7.- Jiménez López, Víctor. Ecuaciones Diferenciales: cómo aprenderlas, cómo enseñarlas. EDITUM, 2000.
8.- Larson, Robert P. Hostetler, Roland E. Cálculo y Geometría Analítica. Volumen 2. McGraw Hill, 1995.
9.- Morris Tenenbaum, Harry Pollard. Ecuaciones Diferenciales Ordinarias. Editorial Dover, 1963.
10.- Quintana, Pedro, Villalobos Eloísa, Cornejo María. Métodos de Solución de Ecuaciones Diferenciales y Aplicaciones. Editorial Reverte, 2008.
11.- R. Kent Nagle, Edward B. Saff, Arthur David Snider. Ecuaciones Diferenciales y Problemas con Valores en la Frontera. Editorial Pearson Educación de México, 2005.
12.- Shepley L. Ross. Ecuaciones Diferenciales. Editorial Reverté, 1992.
13.- Zill, Dennis G. Ecuaciones Diferenciales con Aplicaciones. Grupo Editorial Iberoamérica, 1988.
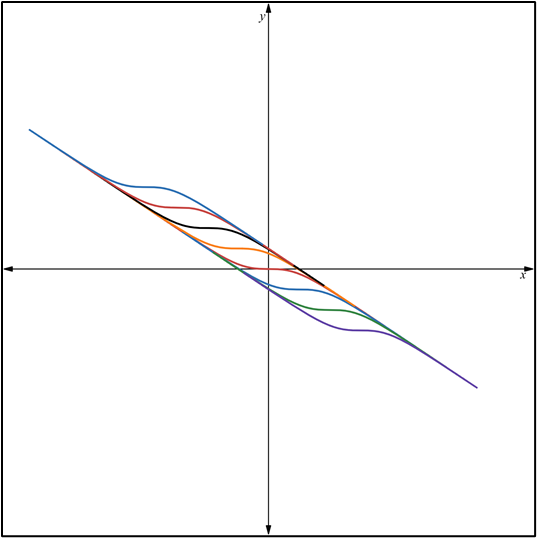
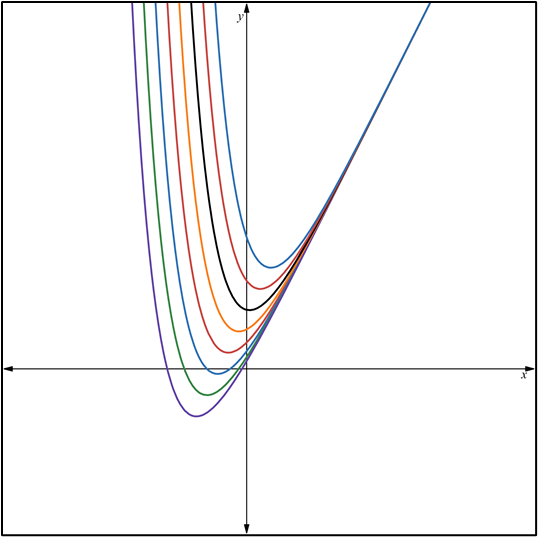
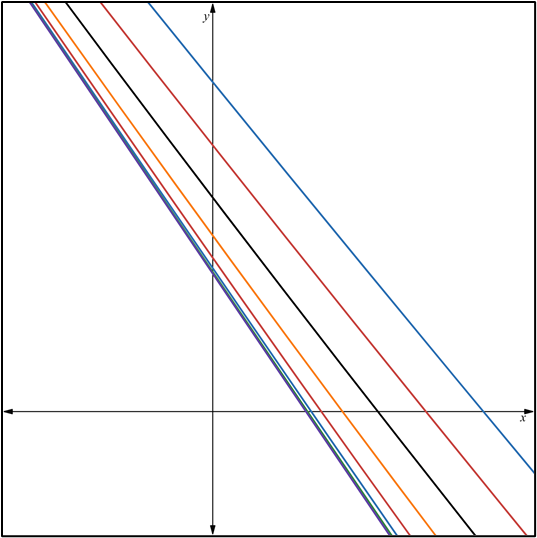
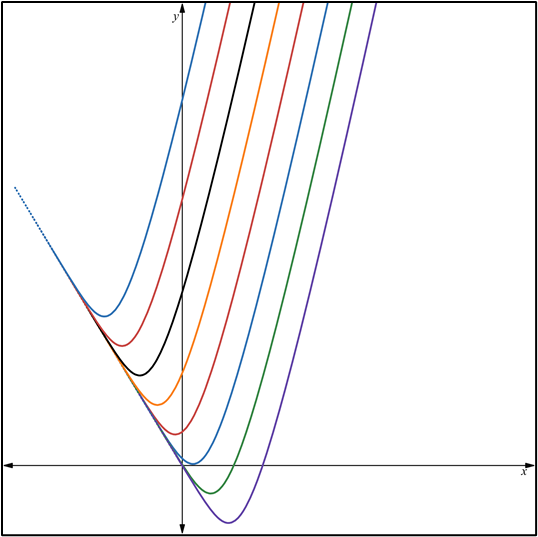
la página web: https://www.desmos.com/calculator/frx7bimvdd?lang=es.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Consider setting @stemsocial as a beneficiary of this post's rewards if you would like to support the community and contribute to its mission of promoting science and education on Hive.